Connectionist Representations of Compositional Structure for Sensor Integration and Situational Awareness in Autonomous Vehicles

ABOUT THE PROJECT

At a glance

To perform a complex behavior such as driving, the human perceptual system builds, maintains, and successively updates a model of the environment. Such a working memory of the environment state is likely to be compositional, so it can be selectively queried before making a decision. For example, before changing into a lane to the left, the working memory should be queried whether there is space in the left lane. Compositional representations are also useful, because they can express an exponentially increasing set of variable combinations in a meaningful data structure, such as the locations, trajectories and identities of objects in the environment. Previous work in robotics and control systems, such as those for simultaneous localization and mapping (SLAM), use compositional representations to describe and interact with the world. However, traditional architectures suffer from issues with computational complexity, approximate computation, inference, data association, and flexible adaptation to the environment (Aulinas, 2008).

Neural networks have recently shown promise in performing complex human-like behaviors, and many are applying such networks to autonomous driving. Learning algorithms and distributed parallel computations present solutions to many challenges faced by traditional robotics control algorithms (Cadena, 2016). However, traditional neural network architectures cannot produce truly compositional representations. As a consequence, most current network architectures for autonomous driving are purely reactive and their decision making process is a black box.

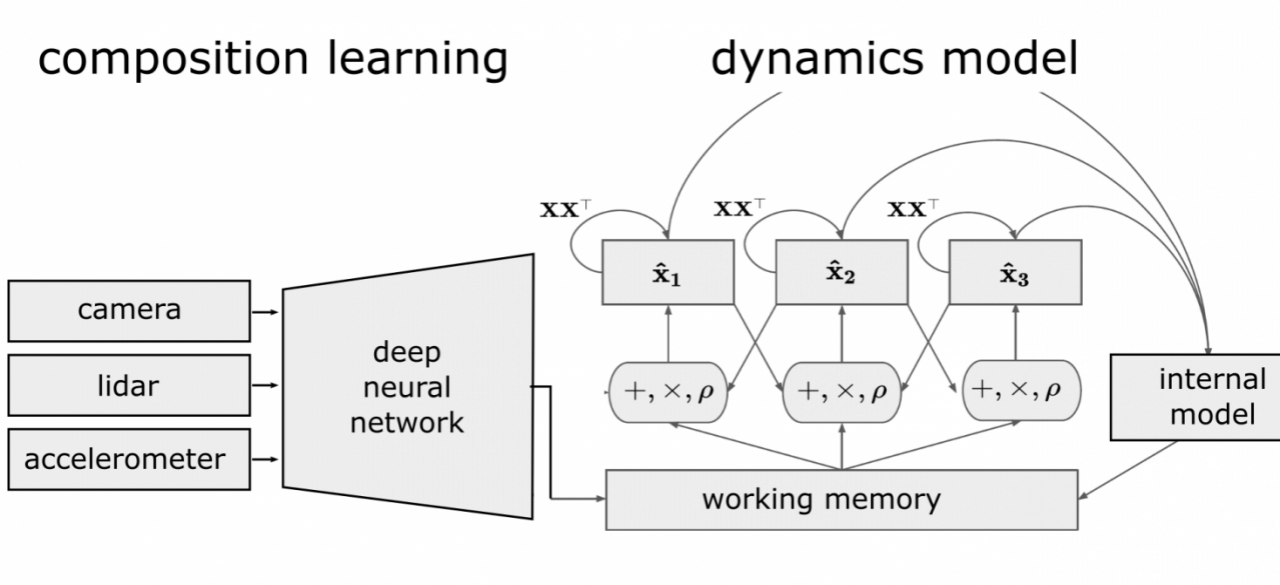
Our project’s goal is to develop a neural network architecture that is capable of compositional situational awareness, as it is relevant for navigation in autonomous vehicles. The idea is that an autonomous agent builds in its working memory a compositional map of its environment. This map will contain a data structure that can answer queries of spatial reasoning. The map can be updated by both sensory input and internal models, and it can be used input to a policy learning network (Mnih, 2015).

Based on frameworks of computing with high-dimensional vectors (Plate, 2003; Kanerva, 2009), our group has recently made progress to enable neural networks to learn and manipulate compositional structure.
Our recent theoretical work (Frady, in press) shows that several frameworks, collectively called Vector Symbolic Architectures (VSA) (Gayler, 2003), are mathematically related and have universal properties, such as working memory capacity. VSAs are formal, comprehensible frameworks for representing information and computing with random high-dimensional vectors, akin to neural population activity. The frameworks include operations, such as superposition (e.g. add), variable binding (e.g. componentwise multiply) and permutation of coordinates, that enables the expression of compositional structure in a distributed representation. Further, VSAs can be used to express symbolic computations in a neural network, which allows integration of traditional robotics architectures for control and cognitive agents (Kawamura, 2006; Eliasmith, 2012).

Our work (Weiss, 2016) extends from the VSA framework Fourier Holographic Reduced Representation (FHRR) (Plate, 2003). We show how to combine deep learning with FHRR to build a compositional representation of a simple scene and perform spatial reasoning. Such a scene consists of several hand-written digits from the MNIST database arranged on a large surface. The network receives glimpses (small visual windows) of this scene focused at different locations. The visual content is indexed with location information by the binding operation, and several glimpses are integrated into working memory. Deep learning is used to update the encoding of each glimpse and to learn to output digit categories from spatial queries. Further work shows how the glimpse locations can be strategically chosen through attention to optimize information about the environment, making computations much more efficient. The working memory can be queried to solve problems of spatial reasoning, such as “what digit is below a 2 and to the left of a 1?” Not only can this network solve such complex reasoning problems, but also each step can be broken down and understood (Fig. 1). Further, this compositional representation can be used in value iteration for path planning by autonomous agents (see Weiss (2016)).

Our goal here will be to build with the described techniques a dynamic working memory relevant to autonomous driving. Consider a system for two-dimensional navigation based on our previous work, which we plan to extend to three-dimensional environments. One population of neurons represents current spatial location of the vehicle in a global reference frame. Our theoretical extensions of FHRR shows how this twodimensional spatial location can be represented as a high-dimensional complex vector: L(t) = Xx(t) × Yy(t),


Figure 1: (a) A compositional working memory is formed to represent the simple scene of digits. (b-d) Heat maps are generated based on which spatial positions satisfy a query to the memory. The combined spatial location can be used to readout the correct digit from the memory.

where X and Y are complex vectors with each element having unit magnitude and random phase, and the exponents x(t) and y(t) are the continuous values of spatial location over time. Raising a complex vector to a continuous power spins the phase of each component, thus creating a distributed encoding of two-dimensional space that varies smoothly over small distances, but produces distinct location vectors for sufficiently separated positions. The neuron ensemble, M(t) is used for the working memory and represents the environment. Another population of neurons, S(t), represents information from image sensors. The map of the environment can be built up over time from sensor data: M(t + 1) = M(t) + L(t) × S(t).

Another goal is to combine information from multiple sensor modalities to update the working-memory. For instance, an update of vehicle location can be made from accelerometer cues as well as from the working memory. The working memory can be queried with sensory input to retrieve an estimate of location, ˆL S(t) = M(t) × S−1(t). Let the population V(t) = Xvx(t) × Yvy(t) represent the instant estimate of velocity, with vx and vy velocity values obtained from accelerometer readings. This can be combined with the current location to get a new location update, ˆLV(t) = L(t) × V(t). In this manner, the network is performing path integration of the velocity signal. The estimates of location from both indexed sensor cues and accelerometer data can be combined through a weighted sum to update the memory, L(t + 1) = SˆLS(t) + VˆLV(t). The weights are from learning algorithms or Bayesian analysis.

Many complex behaviors require simultaneous inference of multiple environment variables, as in SLAM where both the map of the environment and the estimate of location need to be updated together. Previously, we used precise knowledge of the glimpse location to update the memory, rather than simultaneously inferring glimpse location and environment state. To solve such simultaneous inference problems, we have developed a recurrent neural network architecture called resonator circuit based on VSA principles. The resonator circuit is related to and generalizes map-seeking circuits (Arathorn, 2002). It iteratively settles on the best solution to a simultaneuos inference problem, in the case of the map-seeking circuit, object identity and pose. Another project goal will to design resonator circuits to solve the SLAM problem.

Further, resonator circuits are dynamic, and can be used to maintain and update a dynamic internal model of the environment. For instance, the environment model may include a compositional representation of a pedestrian, which contains both the pedestrian’s location and trajectory. The resonator circuit can be used to extract out these components from working-memory, and then recombine the pedestrian’s location and trajectory to update the model (a similar computation to path integration described above). Even in the absence of sensory cues (perhaps the pedestrian becomes temporarily occluded), the resonator circuit can maintain these variables internally and appropriately update the state of the environment in working-memory.

Our poject will start by synthesizing computer generated environments, in which three-dimensional structure is known and can be used as a supervised learning signal. Several simulation environments are now available, such as Mujoco (mujoco.org) or the Unity game engine (unity3d.com). Our project will produce software infrastructure for implementing in GPUs the operations needed for vector computations, as well as infrastructure for integration with simulation environments. In the first year, we will produce several working examples of autonomous agents operating in increasingly complex simulated environments. We will also publish our results for simple environments in scientific journals. Later in year 1, we will begin to explore real sensor data in our framework, and work with other groups, such as Karl Zipser’s group, who are collecting real world data. Throughout year 2, we will continue to expand our work in complexity and build models for the real world, as well as develop software for efficient real-time implementation. The $100K/yr budget consists of $60K/yr funding for post-doc, Paxon Frady, as well as $15K/yr partial funding for graduate students, Eric Weiss (year 1) and Spencer Kent (year 2). Another $15K/yr will fund two PIs for a summer month. Further $10K/yr of funding will be for computer hardware and travel.