CyCADA: Cycle Consistent Adversarial Domain Adaptation

ABOUT THE PROJECT

At a glance

Deep neural networks excel at learning from large amounts of data, but can be poor at generalizing  learned knowledge to new datasets or environments. Even a slight departure from a network's training domain can cause it to make spurious predictions and significantly hurt its performance. The visual domain shift from non-photorealistic synthetic data to real images presents an even more significant challenge.

While we would like to train models on large amounts of synthetic data such as data collected from graphics game engines, such models fail to generalize to real-world imagery. For example, a state-of-the-art semantic segmentation model trained on synthetic dashcam data fails to segment the road in real images, and its overall per-pixel label accuracy drops from 93% (if trained on real imagery) to 54%.

We propose Cycle-Consistent Adversarial Domain Adaptation (CyCADA), which adapts representations at both the pixel-level and feature-level while enforcing pixel and semantic consistency. We use a reconstruction (cycle-consistency) loss to enforce the cross-domain transformation to preserve pixel information and a semantic labeling loss to enforce semantic consistency. CyCADA unifies prior feature-level and image-level adversarial domain adaptation methods together with cycle-consistent image-to-image translation techniques, as illustrated in. It is applicable across a range of deep architectures and/or representation levels, and has several advantages over existing unsupervised domain adaptation methods.

We apply our CyCADA model to the task of digit recognition across domains and the task of semantic segmentation of urban scenes across domains. Experiments show that our model achieves state of the art results on digit adaptation, cross-season adaptation in synthetic data, and on the challenging synthetic-to-real scenario. In the latter case, it improves per-pixel accuracy from 54% to 83%, nearly closing the gap to the target-trained model.

Our experiments confirm  that domain adaptation can benefit greatly from cycle-consistent pixel transformations, and that this is especially important for pixel-level semantic segmentation with contemporary FCN architectures.

 

Continuous and Dynamic Adaptation Networks

Adaptation in its standard form is concerned with adaptation between a fixed set of known domains, typically a single source and target. However, in practice this paradigm is limiting, as different aspects of the real world such as illumination and weather conditions vary continuously and cannot be effectively captured in just two domains alone. We are interested in the development of models that can generalize across a wide variety of domains. Rather than learn a single model for each domain, which quickly becomes intractable as the number of domains grows, we propose learning a single model that is trained to operate in all domains, thereby enabling it to share information between domains.

Standard adaptation approaches fail when attempting to adapt from a single source to many different target domains simultaneously. We propose an adaptation method that exploits the structure between continuously varying domains by adapting in sequence from the source to the most similar target domain. By iterating this process and ensuring that the model continues to consistently classify previously seen examples, we ensure strong performance across all domains with only a single model. Preliminary experiments indicate that our method is applicable in a wide variety of settings, including visual classification and reinforcement learning for playing video games.

We also intend to investigate the use of dynamic networks for continuous domain adaptation. Unlike a standard feed-forward network, which performs a static forward pass regardless of its input, dynamic networks dynamically modify the way they process their input conditioned on the input itself. For example, Gated Mixture of Experts uses an ensemble of "experts" (in our case, networks), combining their activations based on the output of a gating network.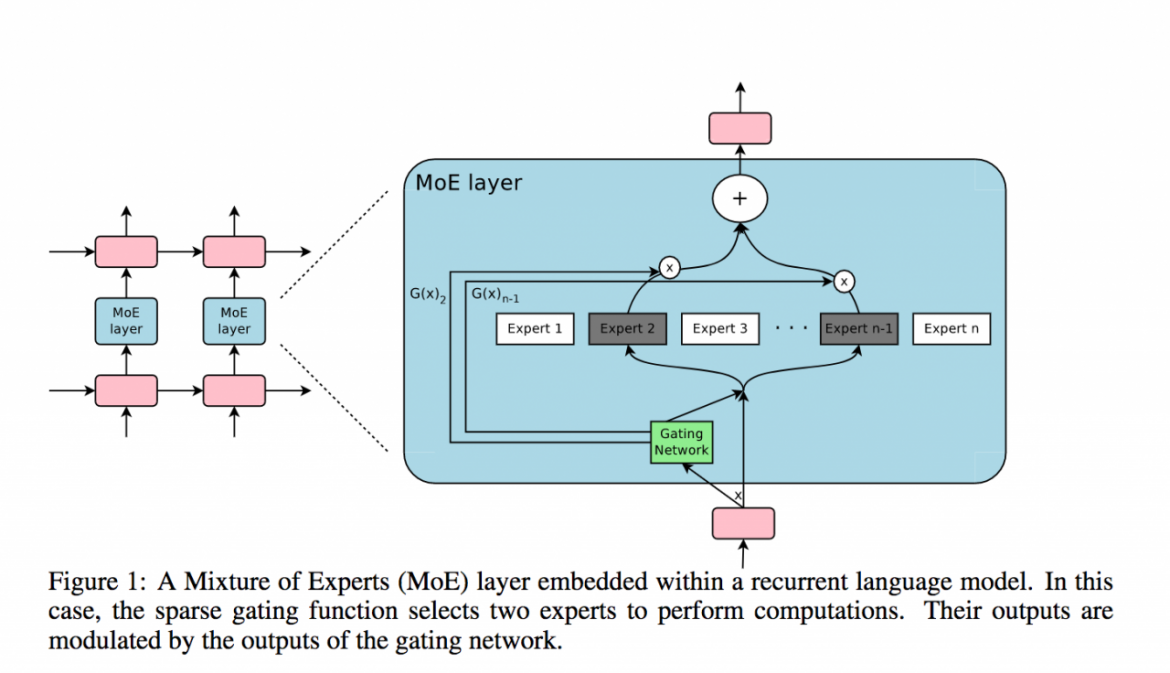

Dynamic Filter Networks use the input to generate the filters and weights for another network that will actually perform a task such as classification.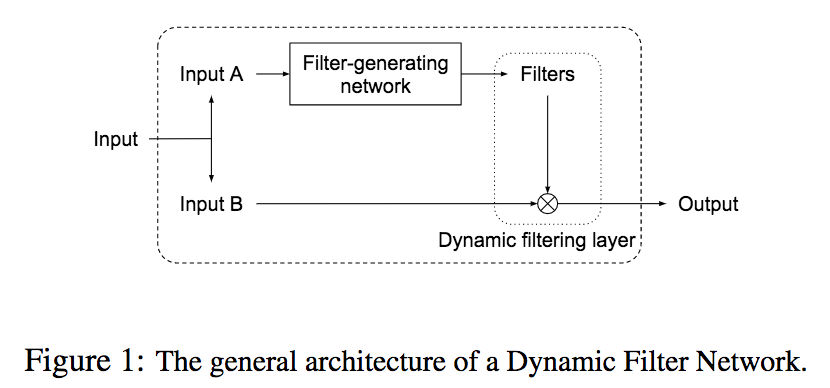


More generally, we are interested in a class of dynamic methods where the actual graph computation performed depends on the domain or instance we are classifying. We propose developing a dynamic method which is capable of generalizing to unseen domains. Our approach will factorize domains into sharable components to allow dynamic recomposition when new combinations of domain factors are encountered, thus enabling continuous adaptation and generalization.