The Dynamical View of Machine Learning Systems

Understanding the generalization capabilities of deep networks and how they handle new data from unfamiliar environments would enable greater confidence in their ability to safely adapt to rare and unseen events. Here we propose casting many of the machine learning algorithms used to train deep networks as controllable dynamical systems, letting us bring the rich literature and intuition from 50 years of control theory to deep network analysis.

Despite the phenomenal success of deep networks, we still lack the ability to reliably prove their robustness, quantify their generalization to new data, and reason about their safety. In contrast, the prediction and control of classical dynamical systems is robust and we have strong guarantees about which controllers will work under which circumstances for which systems. Many of these classical control systems are at work in the modern automobile, ranging from anti-lock brakes to the intricate timing control of the engine.

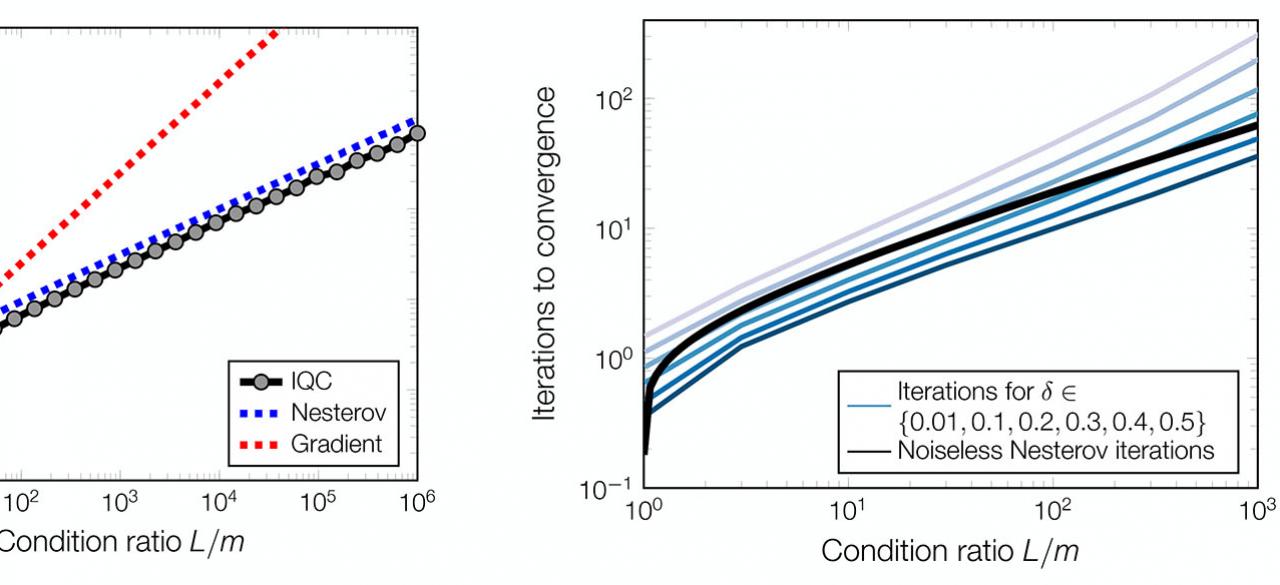
Here we seek to bring this robustness and principled understanding to the algorithms used in deep learning. Recently we have found that a powerful way to bring robustness analysis to algorithms is to view optimization and learning algorithms as dynamical systems. This perspective enables us to apply control theoretic techniques such that multiple objectives including robustness, accuracy, and speed can be seamlessly incorporated in algorithm analysis and design. Indeed, we have shown that the convergence rates of most common algorithms including gradient descent, mirror descent, Nesterov's method, etc. can be verified using a unified set of potential functions. Such potential functions can themselves be found by solving simple optimization problems. These techniques can then be used to search for optimization algorithms with desired performance characteristics. This feedback viewpoint essentially provides a new methodology for algorithm design.